Unlike on the previous slide, this third version of dense matrix multiplication SIMD-izes computation over both A and B instead of just one of them. We are able to make this change due to how matrix multiplication is calculated and properties of the transpose. This is a great example of how mathematical analysis can potentially inform performance optimization decisions in this space. Inverting matrices efficiently is another example where the domains of linear algebra and performance optimization blend nicely.

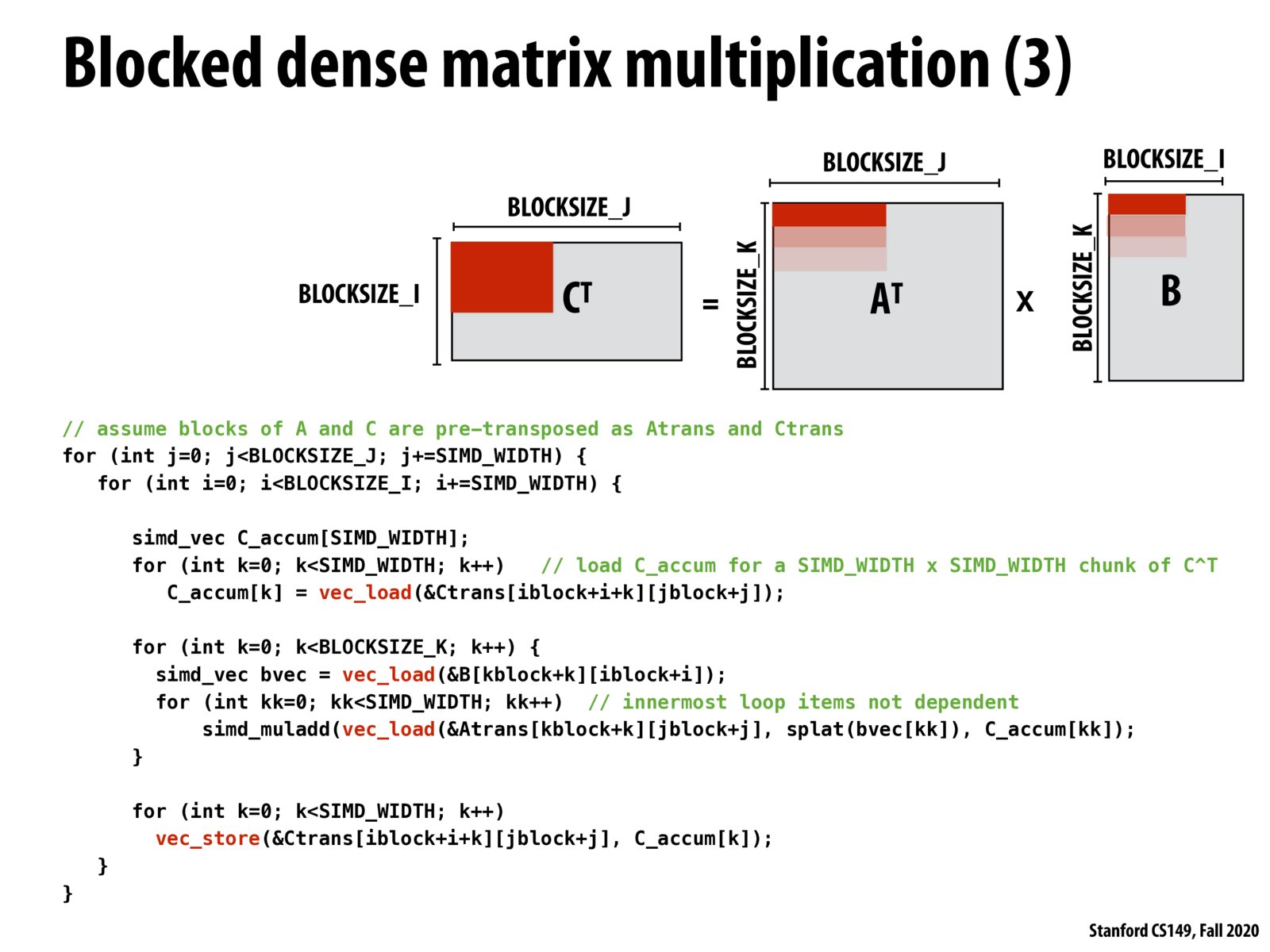
As you've seen the three presented ideas of vectorizing matrix multiplication have their strengths and weaknesses. The first approach attempts to improve the locality of the second array, but if fails when its blocksize doesn't cleanly utilize the SIMD lanes, or because it needs to duplicate elements of the first matrix. The second approach preemtively transposes the second array to get even better spatial locality, but it incurs a transposition overhead. Similarly, this third approach tries to transpose A and C in order to once again maximize locality and utilization, but it just goes to show how a really fast approach to matrix multiplication may need to toggle its approach depending on the dimensions of the matrix. For example, if a matrix is massive, the transposition may be a nontrivial amount of computation / memory usage.